Разработка и применение программного обеспечения в физических исследованиях

Вячеслав Федоров, ИЯФ СО РАН

Для студентов физических специальностей и начинающих ИТ-специалистов, которые хотят познакомиться с Python, Linux, DevOps и SRE.

Цель этой книги — помочь тебе научиться писать более красивые, надёжные и легко сопровождаемые программы для физических исследований. То, о чём мы здесь будем говорить, это не начальный уровень, предполагается, что ты уже знаешь основы физики, минимально умеешь программировать, и хочешь научиться делать это лучше.

И это — отличная цель, к которой мы вместе будем двигаться!

Часто на физических факультетах не уделяется должного внимания IT-дисциплинам, в то время как они очень важны и могут значительно улучшить качество твоих исследований.

В ревью кода моих коллег часто видны результаты того, что в учебных материалах не уделяется отдельное внимание вопросам качества кода. Качество программы и её надёжность страдают — а это гораздо более важные параметры, чем многие поначалу думают. Поначалу кажется, что я написал программу, она в моих идеальных условиях работает и этого достаточно. Но нет, этого недостаточно. Наличие функциональности это одно, а надёжность этой функциональности и качество реализации этой функциональности это совсем другое. То, что мы написали программу и она имеет функциональность — это вовсе не означает, что программа действительно хороша. В этой небольшой книге мы поговорим о том, как разрабатывать, думая не только о функциональности, но и о качестве и надёжности её реализации.

Цели книги:

Познакомиться с основами Linux: Изучить архитектуру операционной системы GNU/Linux, файловые системы, процессы загрузки и методы управления дисками.
Освоить Python: Погрузиться в мир программирования на Python, изучить синтаксис, использование интерактивной оболочки IPython и применять язык для решения физических задач.
Изучить DevOps и SRE: Разобраться в жизненном цикле программного обеспечения, управлении версиями, автоматизации процессов разработки и обеспечения надежности систем.
Научиться работать с базами данных: Понять различные системы управления базами данных (СУБД) и их применение в реальных проектах.
Освоить инструменты для обработки и анализа данных: Изучить библиотеки NumPy, SciPy, Pandas, Matplotlib и другие для эффективного анализа больших данных.
Погрузиться в машинное обучение и нейронные сети: Изучить базовые алгоритмы классификации и основы работы с нейронными сетями для обработки данных физических экспериментов.
Оптимизировать производительность программ: Научиться измерять время выполнения кода, использовать параллельные вычисления и работать с GPU для ускорения обработки данных.

Самое время подписаться: GitHub | Telegram

О себе

Меня зовут Федоров Вячеслав Васильевич, я разработчик программного обеспечения с глубокими знаниями в области физики и вычислительной математики. На протяжении нескольких лет я работаю в Институте ядерной физики им. Будкера, где занимаюсь разработкой наукоемкого прикладного программного обеспечения на языках высокого уровня Python и C++ для решения различных задач. Моя основная работа сосредоточена на моделировании динамики заряженных частиц в сложных электромагнитных полях, а также на внедрении алгоритмов машинного обучения для оптимизации и настройки ускорительных комплексов.

Мой опыт также включает работу в международной компании по разработке ПО и веб-приложений SIBERS, где я руководил командой разработчиков в создании ПО на основе микросервисной архитектуры для государственной организации, оказывающей финансовые услуги. Я активно участвовал в разработке дополнительных модулей для статического анализа кода для различных сред разработки, а также был ведущим разработчиком приложения для врачей, предназначенного для распознавания и присвоения кодов болезней в медицинских картах пациентов с использованием бессерверных вычислений и алгоритмов машинного обучения. Я внедрял процессы автоматизированного тестирования, непрерывной интеграции и доставки кода, проводил обзор и оценку кода, а также подготовил и прочитал полугодовой обучающий курс «Микросервисные масштабируемые веб-сайты» для команды.

Ранее я принимал участие в проектах Роскосмоса, в том числе в разработке ПО на языке C++ для инфракрасного датчика горизонта с использованием платформы Arduino для сверхмалого космического аппарата НГУ «Норби», успешный запуск которого состоялся в 2020 году.

У меня есть диплом бакалавра НГУ в области физики пучков заряженных частиц и физики ускорителей. Я прошёл курсы повышения квалификации по разработке и эксплуатации ПО на Python и C++, алгоритмам и структурам данных, системному администрированию и обеспечению надёжности информационных систем от «Образовательных технологий Яндекса», а также основы искусственного интеллекта и машинного обучения от НГУ.

Мои технические навыки включают: отличное владение языками программирования Python и C++, разнообразными фреймворками; работу с асинхронным и параллельным кодом; проектирование ПО, веб-приложений и микросервисов; создание документации; работу с реляционными базами данных и NoSQL-хранилищами; управление очередями сообщений и задач; владение методологиями непрерывной интеграции и доставки кода, автоматизации процессов сборки, настройки и развёртывания ПО. Мой опыт позволяет ускорять процессы производства IT-продуктов за счёт поиска и устранения «узких» мест, автоматизировать процесс разработки и развёртывания приложений, контейнеризировать приложения и размещать их в облачных сервисах. Я использую актуальные инструменты для обеспечения качества, скорости и стабильности приложений, управляю инфраструктурой в парадигме Infrastructure as Code, сокращая время команды на развёртывание и масштабирование, а также налаживаю коммуникацию между участниками процесса разработки продукта: службой эксплуатации, разработчиками, заказчиками от бизнеса и многими другими.

Больше обо мне можно узнать здесь

Применение ИИ для разработки ПО

Сначала поговорим о теме, которая стремительно меняет ландшафт разработки программного обеспечения — о применении Искусственного Интеллекта.

Особый акцент мы сделаем на том, как эти технологии могут быть применены для разработки ПО.

Почему именно сейчас? Контекст и скорость изменений

Подготовка лекции

Готовить лекцию об ИИ в разработке — неблагодарное дело. Материал устаревает быстрее, чем успеваешь дописать слайд. То, что было актуально месяц назад, сегодня уже может считаться «устаревшим». Это прямое следствие экспоненциального прогресса в области, о котором часто говорит, например, Сэм Альтман:

Мы прошли горизонт событий; взлет начался.

blog.samaltman.com

Технологическая сингулярность и экспоненциальный прогресс

Концепция сингулярности — это точка, после которой технологический рост становится непредсказуемым и необратимым для нас. Со стороны кажется, что прогресс взрывной и мгновенный, но на самом деле он растянут во времени — мы просто не замечали его до определенного момента.

История развития ИИ: маховик раскручивался давно

Текущий бум — не случайность. Маховик начал раскручиваться давно:

2014-2015 гг.: Прорыв в области Generative Adversarial Networks (GAN), трансформеров.
2018-2020 гг.: Появление и scaling больших языковых моделей (LLM) — GPT-2, GPT-3.
2022 г.: Выход ChatGPT стал точкой взрыва популярности.

Рост популярности ChatGPT и инвестиции

ChatGPT набрал миллион пользователей за 5 дней. Для сравнения: Netflix потребовалось 3.5 года, Airbnb — 2.5 года, Instagram — 2.5 месяца. Это беспрецедентная скорость.

За этим последовали и беспрецедентные инвестиции:

Рынок LLM-моделей растет двузначными числами.
Проекты вроде StarGate (предполагаемый совместный дата-центр Microsoft и OpenAI стоимостью в $100 млрд).
Прогнозы роста мирового ВВП за счет ИИ исчисляются триллионами долларов.

chatgpt-statistics

Stargate

Зачем?

https://epoch.ai/gradient-updates/ai-and-explosive-growth-redux

ИИ и разработчик: данные и реалии

Использование ИИ разработчиками

Опросы показывают, что около 65% разработчиков уже используют чат-боты в своей работе.

survey.stackoverflow.co

Преувеличение возможностей ИИ

Существует важное исследование, которое часто упускают из виду:

Разработчики склонны преувеличивать, насколько ИИ может помочь.
В контролируемых экспериментах использование ИИ ухудшало время выполнения задач.
Группа, которая не использовала ИИ, справлялась с задачами быстрее.

Вывод: ИИ — не волшебная таблетка. Это инструмент, эффективность которого зависит от навыка его использования.

2025-07-10-early-2025-ai-experienced-os-dev-study

Как это работает? Технические основы

Основы нейросетей

Упрощенно, в основе современных LLM лежит операция перемножения матриц. Модель — это граф с:

Входным слоем (ваш промт, контекст).
Множеством скрытых (промежуточных) слоев.
Выходным слоем (ответ модели).

wiki/Neural_network

Провайдеры и модели

Существует множество провайдеров: OpenAI (GPT), Anthropic (Claude), Google (Gemini), Meta (Llama), Mistral и многие другие. У каждого — своя линейка моделей разного размера и capability.

openrouter.ai/rankings

Характеристики моделей

Размер: Современные крупные модели имеют более триллиона параметров. Это позволяет им предсказывать не только следующее слово, но и сложные смысловые конструкции.
Контекстное окно: Определяет объем текста (в токенах), который модель может «увидеть» за раз. Критически важно для работы с большими кодовыми базами. Размер токена зависит от языка (~1 токен = 0.75 слова на англ., ~1-2 символа на русск.).
Размышляющие модели (Reasoning): Модели, которые учатся делать последовательные выводы, дополняя контекст своими «рассуждениями».

artificialanalysis

Подходы к работе с LLM

Промтинг:
- Zero-shot: Просто задать вопрос.
- One-shot: Дать пример ответа.
- Chain-of-thought: Попросить модель рассуждать шаг за шагом.
Контекст-инжиниринг: Наиболее важен для разработки. Это искусство подачи модели релевантного контекста (вашего кода, документации, спецификации) для получения точного ответа. Важнее, чем идеальный промт.

prompt-engineering

context-engineering

Агенты

Агент — это LLM, помещенная в цикл принятия решений, с доступом к инструментам (Tools).

Агентная система сама решает, какой инструмент вызвать, вызывает его, получает результат и передает его обратно модели.
Именно агенты превращают LLM из «болтушки» в мощный инструмент для автоматизации разработки.

building-effective-agents

Инструментарий: Кодинг-агенты на практике

Введение в кодинг-агенты

Большинство современных кодинг-агентов — это, по сути, форки редактора VS Code с интегрированным ИИ-ассистентом. Популярные примеры: Cursor, Windsurf, Codeium, Aider.

Аналогия: как есть ОС Windows, macOS, Linux — так же есть и VS Code, Cursor, Zed. Каждый со своими фичами.

Типы помощников

Ассистенты (Плагины): Например, GitHub Copilot, Amazon Q, CodeWhisperer. Работают внутри вашей IDE.
Терминальные агенты: aider, windsurf, claude-cli. Работают прямо в терминале, мощны для работы с целыми репозиториями.
Автономные агенты (Cursor): Полноценная среда разработки, «заточенная» под работу с ИИ.

Обзор возможностей

Автокомплит: Модель предлагает продолжение кода по ходу его написания.
Редактирование в файле: Можно выделить блок кода и дать команду («добавь проверку ошибок здесь»).
Чат: Окно для диалога с моделью. Можно добавлять контекст всего проекта.
Агентный режим: Модель сама планирует и выполняет задачи, используя инструменты (написание, запуск кода, чтение ошибок).

Правила и контекст

Правила (rules): Можно описать архитектурные особенности проекта, код-стайл, требования. Агент будет следовать им.
- Пример правила: «Все коммиты, сделанные агентом, должны иметь префикс [AI] в сообщении».
Ignore: Аналог .gitignore. Позволяет защитить чувствительные данные и секреты от отправки модели.

MCP (Model Context Protocol)

Унифицированный протокол от OpenAI для подключения любых инструментов к любым совместимым клиентам (например, Cursor).
Позволяет агенту работать с вашей БД, API, файловой системой, системой управления задачами и т.д.
Ключевая технология для создания мощных кастомных агентов под специфические задачи (например, для анализа видео с камер установки).

Вопросы и ответы

Q: Какая модель сейчас лучшая по соотношению цена/качество для разработки? A: Однозначного ответа нет. Claude 3.5 Sonnet показывает отличные результаты для кода. Из opensource сильна DeepSeek Coder-V2. Важно тестировать на своих задачах. Скорость и стоимость токенов — ключевые факторы.

Q: Сложно ли интегрировать это в большой legacy-проект? A: Да, сложность интеграции напрямую зависит от размера кодовой базы и количества кастомных инструментов. MCP — лучший друг в этом случае. Терминальные агенты (aider) часто справляются с большими проектами лучше, чем GUI-ассистенты.

Q: Может ли ИИ породить нестандартное решение, как джуниор-разработчик? A: Нет, в этом его ограничение. ИИ оперирует усредненными паттернами из своих тренировочных данных. Он гениален в шаблонных задачах, но не в изобретении принципиально новых парадигм. Его сила — скорость и объем, а не креативность.

Q: Как начать использовать это эффективно в научных проектах? A: Начните с малого:

Поручите ИИ писать шаблонный код (парсеры логов, скрипты для предобработки видео).
Используйте его для документирования вашего кода.
Попробуйте сгенерировать визуализацию для ваших данных.
Постепенно внедряйте агентов для автоматизации рутины (например, запуск расчетов, сбор результатов).

Python Tutorial

Python is a great general-purpose programming language on its own, but with the help of a few popular libraries (numpy, scipy, matplotlib and holoviews) it becomes a powerful environment for scientific computing.

We expect that many of you will have some experience with Python and Numpy; for the rest of you, this section will serve as a quick crash course both on the Python programming language and on the use of Python for scientific computing.

In this tutorial, we will cover:

Basic Python: Basic data types, Functions, Classes
Numpy: Arrays, Array indexing, Datatypes, Array math, Broadcasting
Matplotlib: Plotting, Subplots, Images
IPython: Creating notebooks, Typical workflows

Basics of Python

Python is a high-level, dynamically typed multiparadigm programming language. Python code is often said to be almost like pseudocode, since it allows you to express very powerful ideas in very few lines of code while being very readable.

We recommend to read PEP 8.

Python versions and Zen of Python

There are currently supported versions of Python 3.X. Support for Python 2.7 ended in 2020. For this class all code will use Python 3.7.

You can check your Python version at the command line by running python --version.

!python --version

Python 3.7.4

import this

The Zen of Python, by Tim Peters

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!

Basic data types

Numbers

Integers and floats work as you would expect from other languages:

x = 3
print(x, type(x))

3 <class 'int'>

print(x + 1)   # Addition;
print(x - 1)   # Subtraction;
print(x * 2)   # Multiplication;
print(x ** 2)  # Exponentiation;

x += 1
print(x)  # Prints "4"
x *= 2
print(x)  # Prints "8"

4
8

y = 2.5
print(type(y)) # Prints "<type 'float'>"
print(y, y + 1, y * 2, y ** 2) # Prints "2.5 3.5 5.0 6.25"

<class 'float'>
2.5 3.5 5.0 6.25

Note that unlike many languages, Python does not have unary increment (x++) or decrement (x--) operators.

Python also has built-in types for long integers and complex numbers; you can find all of the details in the documentation.

Booleans

Python implements all of the usual operators for Boolean logic, but uses English words rather than symbols (&&, ||, etc.):

T, F = True, False
print(type(T)) # Prints "<type 'bool'>"

<class 'bool'>

Now we let's look at the operations:

print(T and F) # Logical AND;
print(T or F)  # Logical OR;
print(not T)   # Logical NOT;
print(T != F)  # Logical XOR;

False
True
False
True

Strings

hello = 'hello'   # String literals can use single quotes
world = "world"   # or double quotes; it does not matter.
print(hello, len(hello))

hello 5

hw = hello + ' ' + world  # String concatenation
print(hw)  # prints "hello world"

hello world

hw12 = '%s %s %d' % (hello, world, 12)  # sprintf style string formatting
print(hw12)  # prints "hello world 12"

hello world 12

String objects have a bunch of useful methods; for example:

s = "hello"
print(s.capitalize())  # Capitalize a string; prints "Hello"
print(s.upper())       # Convert a string to uppercase; prints "HELLO"
print(s.rjust(7))      # Right-justify a string, padding with spaces; prints "  hello"
print(s.center(7))     # Center a string, padding with spaces; prints " hello "
print(s.replace('l', '(ell)'))  # Replace all instances of one substring with another;
                               # prints "he(ell)(ell)o"
print('  world '.strip())  # Strip leading and trailing whitespace; prints "world"

Hello
HELLO
  hello
 hello 
he(ell)(ell)o
world

You can find a list of all string methods in the documentation.

Containers

Python includes several built-in container types: lists, dictionaries, sets, and tuples.

Lists

A list is the Python equivalent of an array, but is resizeable and can contain elements of different types:

xs = [3, 1, 2]   # Create a list
print(xs, xs[2])
print(xs[-1])     # Negative indices count from the end of the list; prints "2"

[3, 1, 2] 2
2

xs[2] = 'foo'    # Lists can contain elements of different types
print(xs)

[3, 1, 'foo']

xs.append('bar') # Add a new element to the end of the list
print(xs)

[3, 1, 'foo', 'bar']

x = xs.pop()     # Remove and return the last element of the list
print(x, xs)

bar [3, 1, 'foo']

As usual, you can find all the gory details about lists in the documentation.

Slicing

In addition to accessing list elements one at a time, Python provides concise syntax to access sublists; this is known as slicing:

nums = range(5)    # range is a built-in function that creates a list of integers
print(nums)         # Prints "[0, 1, 2, 3, 4]"
print(nums[2:4])    # Get a slice from index 2 to 4 (exclusive); prints "[2, 3]"
print(nums[2:])     # Get a slice from index 2 to the end; prints "[2, 3, 4]"
print(nums[:2])     # Get a slice from the start to index 2 (exclusive); prints "[0, 1]"
print(nums[:])      # Get a slice of the whole list; prints ["0, 1, 2, 3, 4]"
print(nums[:-1])    # Slice indices can be negative; prints ["0, 1, 2, 3]"

range(0, 5)
range(2, 4)
range(2, 5)
range(0, 2)
range(0, 5)
range(0, 4)

Loops

You can loop over the elements of a list like this:

animals = ['cat', 'dog', 'monkey']
for animal in animals:
    print(animal)

cat
dog
monkey

If you want access to the index of each element within the body of a loop, use the built-in enumerate function:

animals = ['cat', 'dog', 'monkey']
for idx, animal in enumerate(animals):
    print('#%d: %s' % (idx + 1, animal))

#1: cat
#2: dog
#3: monkey

List comprehensions:

When programming, frequently we want to transform one type of data into another. As a simple example, consider the following code that computes square numbers:

nums = [0, 1, 2, 3, 4]
squares = []
for x in nums:
    squares.append(x ** 2)
print(squares)

[0, 1, 4, 9, 16]

You can make this code simpler using a list comprehension:

nums = [0, 1, 2, 3, 4]
squares = [x ** 2 for x in nums]
print(squares)

[0, 1, 4, 9, 16]

List comprehensions can also contain conditions:

nums = [0, 1, 2, 3, 4]
even_squares = [x ** 2 for x in nums if x % 2 == 0]
print(even_squares)

[0, 4, 16]

Dictionaries

A dictionary stores (key, value) pairs, similar to a Map in Java or an object in Javascript. You can use it like this:

d = {'cat': 'cute', 'dog': 'furry'}  # Create a new dictionary with some data
print(d['cat'])       # Get an entry from a dictionary; prints "cute"
print('cat' in d)     # Check if a dictionary has a given key; prints "True"

cute
True

d['fish'] = 'wet'    # Set an entry in a dictionary
print(d['fish'])      # Prints "wet"

wet

print(d.get('monkey', 'N/A'))  # Get an element with a default; prints "N/A"
print(d.get('fish', 'N/A'))   # Get an element with a default; prints "wet"

N/A
wet

del d['fish']        # Remove an element from a dictionary
print(d.get('fish', 'N/A')) # "fish" is no longer a key; prints "N/A"

N/A

You can find all you need to know about dictionaries in the documentation.

It is easy to iterate over the keys in a dictionary:

d = {'person': 2, 'cat': 4, 'spider': 8}
for animal in d:
    legs = d[animal]
    print('A %s has %d legs' % (animal, legs))

A person has 2 legs
A cat has 4 legs
A spider has 8 legs

Dictionary comprehensions: These are similar to list comprehensions, but allow you to easily construct dictionaries. For example:

nums = [0, 1, 2, 3, 4]
even_num_to_square = {x: x ** 2 for x in nums if x % 2 == 0}
print(even_num_to_square)

{0: 0, 2: 4, 4: 16}

Sets

A set is an unordered collection of distinct elements. As a simple example, consider the following:

animals = {'cat', 'dog'}
print('cat' in animals)   # Check if an element is in a set; prints "True"
print('fish' in animals)  # prints "False"

True
False

animals.add('fish')      # Add an element to a set
print('fish' in animals)
print(len(animals))       # Number of elements in a set;

True
3

animals.add('cat')       # Adding an element that is already in the set does nothing
print(len(animals))       
animals.remove('cat')    # Remove an element from a set
print(len(animals))

3
2

Loops: Iterating over a set has the same syntax as iterating over a list; however since sets are unordered, you cannot make assumptions about the order in which you visit the elements of the set:

animals = {'cat', 'dog', 'fish'}
for idx, animal in enumerate(animals):
    print('#%d: %s' % (idx + 1, animal))
# Prints "#1: fish", "#2: dog", "#3: cat"

#1: fish
#2: dog
#3: cat

Set comprehensions: Like lists and dictionaries, we can easily construct sets using set comprehensions:

from math import sqrt
print({int(sqrt(x)) for x in range(30)})

{0, 1, 2, 3, 4, 5}

Tuples

A tuple is an (immutable) ordered list of values. A tuple is in many ways similar to a list; one of the most important differences is that tuples can be used as keys in dictionaries and as elements of sets, while lists cannot. Here is a trivial example:

d = {(x, x + 1): x for x in range(10)}  # Create a dictionary with tuple keys
t = (5, 6)       # Create a tuple
print(type(t))
print(d[t])       
print(d[(1, 2)])

<class 'tuple'>
5
1

Functions

Python functions are defined using the def keyword. For example:

def sign(x: float) -> str:
    '''Function sign''' # document line
    
    if x > 0:
        return 'positive'
    elif x < 0:
        return 'negative'
    else:
        return 'zero'

for x in [-1, 0, 1]:
    print(sign(x))

negative
zero
positive

help(sign)

Help on function sign in module __main__:

sign(x: float) -> str
    Function sign

We will often define functions to take optional keyword arguments, like this:

def hello(name: str, loud: bool=False) -> None:
    '''Function hello
    
    If loud is True, 
    then the name is printed in capital letters.
    '''
    
    if loud:
        print('HELLO, %s' % name.upper())
    else:
        print('Hello, %s!' % name)

hello('Bob')
hello('Fred', loud=True)

Hello, Bob!
HELLO, FRED

help(hello)

Help on function hello in module __main__:

hello(name: str, loud: bool = False) -> None
    Function hello
    
    If loud is True, 
    then the name is printed in capital letters.

Classes

The syntax for defining classes in Python is straightforward:

class Greeter:
    '''Class Greeter
    
    method greet:
    If loud is True, 
    then the name is printed in capital letters.
    '''

    # Constructor
    def __init__(self, name):
        self.name = name  # Create an instance variable

    # Instance method
    def greet(self, loud: bool=False) ->None:
        if loud:
            print('HELLO, %s!' % self.name.upper())
        else:
            print('Hello, %s' % self.name)

g = Greeter('Fred')  # Construct an instance of the Greeter class
g.greet()            # Call an instance method; prints "Hello, Fred"
g.greet(loud=True)   # Call an instance method; prints "HELLO, FRED!"

Hello, Fred
HELLO, FRED!

help(Greeter)

Help on class Greeter in module __main__:

class Greeter(builtins.object)
 |  Greeter(name)
 |  
 |  Class Greeter
 |  
 |  method greet:
 |  If loud is True, 
 |  then the name is printed in capital letters.
 |  
 |  Methods defined here:
 |  
 |  __init__(self, name)
 |      Initialize self.  See help(type(self)) for accurate signature.
 |  
 |  greet(self, loud: bool = False) -> None
 |      # Instance method
 |  
 |  ----------------------------------------------------------------------
 |  Data descriptors defined here:
 |  
 |  __dict__
 |      dictionary for instance variables (if defined)
 |  
 |  __weakref__
 |      list of weak references to the object (if defined)

Numpy

Numpy is the core library for scientific computing in Python. It provides a high-performance multidimensional array object, and tools for working with these arrays.

To use Numpy, we first need to import the numpy package:

import numpy as np

Arrays

A numpy array is a grid of values, all of the same type, and is indexed by a tuple of nonnegative integers. The number of dimensions is the rank of the array; the shape of an array is a tuple of integers giving the size of the array along each dimension.

We can initialize numpy arrays from nested Python lists, and access elements using square brackets:

a = np.array([1, 2, 3])  # Create a rank 1 array
print(type(a), a.shape, a[0], a[1], a[2])
a[0] = 5                 # Change an element of the array
print(a)

<class 'numpy.ndarray'> (3,) 1 2 3
[5 2 3]

b = np.array([[1,2,3],[4,5,6]])   # Create a rank 2 array
print(b)

[[1 2 3]
 [4 5 6]]

print(b.shape)                   
print(b[0, 0], b[0, 1], b[1, 0])

(2, 3)
1 2 4

Numpy also provides many functions to create arrays:

a = np.zeros((2,2))  # Create an array of all zeros
print(a)

[[0. 0.]
 [0. 0.]]

b = np.ones((1,2))   # Create an array of all ones
print(b)

[[1. 1.]]

c = np.full((2,2), 7) # Create a constant array
print(c)

[[7 7]
 [7 7]]

d = np.eye(2)        # Create a 2x2 identity matrix
print(d)

[[1. 0.]
 [0. 1.]]

e = np.random.random((2,2)) # Create an array filled with random values
print(e)

[[0.57584699 0.0757792 ]
 [0.18793454 0.78004389]]

Array indexing

Numpy offers several ways to index into arrays.

Slicing: Similar to Python lists, numpy arrays can be sliced. Since arrays may be multidimensional, you must specify a slice for each dimension of the array:

import numpy as np

# Create the following rank 2 array with shape (3, 4)
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])

# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
#  [6 7]]
b = a[:2, 1:3]
print(b)

[[2 3]
 [6 7]]

A slice of an array is a view into the same data, so modifying it will modify the original array.

print(a[0, 1])  
b[0, 0] = 77    # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1])

2
77

You can also mix integer indexing with slice indexing. However, doing so will yield an array of lower rank than the original array.

# Create the following rank 2 array with shape (3, 4)
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
print(a)

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]

Two ways of accessing the data in the middle row of the array. Mixing integer indexing with slices yields an array of lower rank, while using only slices yields an array of the same rank as the original array:

row_r1 = a[1, :]    # Rank 1 view of the second row of a  
row_r2 = a[1:2, :]  # Rank 2 view of the second row of a
row_r3 = a[[1], :]  # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) 
print(row_r2, row_r2.shape)
print(row_r3, row_r3.shape)

[5 6 7 8] (4,)
[[5 6 7 8]] (1, 4)
[[5 6 7 8]] (1, 4)

# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape)
print(col_r2, col_r2.shape)

[ 2  6 10] (3,)
[[ 2]
 [ 6]
 [10]] (3, 1)

Integer array indexing: When you index into numpy arrays using slicing, the resulting array view will always be a subarray of the original array. In contrast, integer array indexing allows you to construct arbitrary arrays using the data from another array. Here is an example:

a = np.array([[1,2], [3, 4], [5, 6]])

# An example of integer array indexing.
# The returned array will have shape (3,) and 
print(a[[0, 1, 2], [0, 1, 0]])

# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]]))

[1 4 5]
[1 4 5]

# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]])

# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]]))

[2 2]
[2 2]

One useful trick with integer array indexing is selecting or mutating one element from each row of a matrix:

# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a)

[[ 1  2  3]
 [ 4  5  6]
 [ 7  8  9]
 [10 11 12]]

# Create an array of indices
b = np.array([0, 2, 0, 1])

# Select one element from each row of a using the indices in b
print(a[np.arange(4), b])  # Prints "[ 1  6  7 11]"

[ 1  6  7 11]

# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a)

[[11  2  3]
 [ 4  5 16]
 [17  8  9]
 [10 21 12]]

Boolean array indexing: Boolean array indexing lets you pick out arbitrary elements of an array. Frequently this type of indexing is used to select the elements of an array that satisfy some condition. Here is an example:

import numpy as np

a = np.array([[1,2], [3, 4], [5, 6]])

bool_idx = (a > 2)  # Find the elements of a that are bigger than 2;
                    # this returns a numpy array of Booleans of the same
                    # shape as a, where each slot of bool_idx tells
                    # whether that element of a is > 2.

print(bool_idx)

[[False False]
 [ True  True]
 [ True  True]]

# We use boolean array indexing to construct a rank 1 array
# consisting of the elements of a corresponding to the True values
# of bool_idx
print(a[bool_idx])

# We can do all of the above in a single concise statement:
print(a[a > 2])

[3 4 5 6]
[3 4 5 6]

For brevity we have left out a lot of details about numpy array indexing; if you want to know more you should read the documentation.

Datatypes

Every numpy array is a grid of elements of the same type. Numpy provides a large set of numeric datatypes that you can use to construct arrays. Numpy tries to guess a datatype when you create an array, but functions that construct arrays usually also include an optional argument to explicitly specify the datatype. Here is an example:

x = np.array([1, 2])  # Let numpy choose the datatype
y = np.array([1.0, 2.0])  # Let numpy choose the datatype
z = np.array([1, 2], dtype=np.int64)  # Force a particular datatype

print(x.dtype, y.dtype, z.dtype)

int64 float64 int64

You can read all about numpy datatypes in the documentation.

Array math

Basic mathematical functions operate elementwise on arrays, and are available both as operator overloads and as functions in the numpy module:

x = np.array([[1,2],[3,4]], dtype=np.float64)
y = np.array([[5,6],[7,8]], dtype=np.float64)

# Elementwise sum; both produce the array
print(x + y)
print(np.add(x, y))

[[ 6.  8.]
 [10. 12.]]
[[ 6.  8.]
 [10. 12.]]

# Elementwise difference; both produce the array
print(x - y)
print(np.subtract(x, y))

[[-4. -4.]
 [-4. -4.]]
[[-4. -4.]
 [-4. -4.]]

# Elementwise product; both produce the array
print(x * y)
print(np.multiply(x, y))

[[ 5. 12.]
 [21. 32.]]
[[ 5. 12.]
 [21. 32.]]

# Elementwise division; both produce the array
# [[ 0.2         0.33333333]
#  [ 0.42857143  0.5       ]]
print(x / y)
print(np.divide(x, y))

[[0.2        0.33333333]
 [0.42857143 0.5       ]]
[[0.2        0.33333333]
 [0.42857143 0.5       ]]

# Elementwise square root; produces the array
# [[ 1.          1.41421356]
#  [ 1.73205081  2.        ]]
print(np.sqrt(x))

[[1.         1.41421356]
 [1.73205081 2.        ]]

Note that unlike MATLAB, * is elementwise multiplication, not matrix multiplication. We instead use the dot function to compute inner products of vectors, to multiply a vector by a matrix, and to multiply matrices. dot is available both as a function in the numpy module and as an instance method of array objects:

x = np.array([[1,2],[3,4]])
y = np.array([[5,6],[7,8]])

v = np.array([9,10])
w = np.array([11, 12])

# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))

219
219

# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))

[29 67]
[29 67]

# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
#  [43 50]]
print(x.dot(y))
print(np.dot(x, y))

[[19 22]
 [43 50]]
[[19 22]
 [43 50]]

Numpy provides many useful functions for performing computations on arrays; one of the most useful is sum:

x = np.array([[1,2],[3,4]])

print(np.sum(x))  # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0))  # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1))  # Compute sum of each row; prints "[3 7]"

10
[4 6]
[3 7]

You can find the full list of mathematical functions provided by numpy in the documentation.

Apart from computing mathematical functions using arrays, we frequently need to reshape or otherwise manipulate data in arrays. The simplest example of this type of operation is transposing a matrix; to transpose a matrix, simply use the T attribute of an array object:

print(x)
print(x.T)

[[1 2]
 [3 4]]
[[1 3]
 [2 4]]

v = np.array([[1,2,3]])
print(v) 
print(v.T)

[[1 2 3]]
[[1]
 [2]
 [3]]

Broadcasting

Broadcasting is a powerful mechanism that allows numpy to work with arrays of different shapes when performing arithmetic operations. Frequently we have a smaller array and a larger array, and we want to use the smaller array multiple times to perform some operation on the larger array.

For example, suppose that we want to add a constant vector to each row of a matrix. We could do it like this:

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x)   # Create an empty matrix with the same shape as x

# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
    y[i, :] = x[i, :] + v

print(y)

[[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]

This works; however when the matrix x is very large, computing an explicit loop in Python could be slow. Note that adding the vector v to each row of the matrix x is equivalent to forming a matrix vv by stacking multiple copies of v vertically, then performing elementwise summation of x and vv. We could implement this approach like this:

vv = np.tile(v, (4, 1))  # Stack 4 copies of v on top of each other
print(vv)                 # Prints "[[1 0 1]
                         #          [1 0 1]
                         #          [1 0 1]
                         #          [1 0 1]]"

[[1 0 1]
 [1 0 1]
 [1 0 1]
 [1 0 1]]

y = x + vv  # Add x and vv elementwise
print(y)

[[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]

Numpy broadcasting allows us to perform this computation without actually creating multiple copies of v. Consider this version, using broadcasting:

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v  # Add v to each row of x using broadcasting
print(y)

[[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]

The line y = x + v works even though x has shape (4, 3) and v has shape (3,) due to broadcasting; this line works as if v actually had shape (4, 3), where each row was a copy of v, and the sum was performed elementwise.

Broadcasting two arrays together follows these rules:

If the arrays do not have the same rank, prepend the shape of the lower rank array with 1s until both shapes have the same length.
The two arrays are said to be compatible in a dimension if they have the same size in the dimension, or if one of the arrays has size 1 in that dimension.
The arrays can be broadcast together if they are compatible in all dimensions.
After broadcasting, each array behaves as if it had shape equal to the elementwise maximum of shapes of the two input arrays.
In any dimension where one array had size 1 and the other array had size greater than 1, the first array behaves as if it were copied along that dimension

If this explanation does not make sense, try reading the explanation from the documentation.

Functions that support broadcasting are known as universal functions. You can find the list of all universal functions in the documentation.

Here are some applications of broadcasting:

# Compute outer product of vectors
v = np.array([1,2,3])  # v has shape (3,)
w = np.array([4,5])    # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:

print(np.reshape(v, (3, 1)) * w)

[[ 4  5]
 [ 8 10]
 [12 15]]

# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:

print(x + v)

[[2 4 6]
 [5 7 9]]

# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:

print((x.T + w).T)

[[ 5  6  7]
 [ 9 10 11]]

# Another solution is to reshape w to be a row vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))

[[ 5  6  7]
 [ 9 10 11]]

# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
print(x * 2)

[[ 2  4  6]
 [ 8 10 12]]

Broadcasting typically makes your code more concise and faster, so you should strive to use it where possible.

This brief overview has touched on many of the important things that you need to know about numpy, but is far from complete. Check out the numpy reference to find out much more about numpy.

Scipy

To be continued...

Matplotlib

Matplotlib is a plotting library. In this section give a brief introduction to the matplotlib.pyplot module, which provides a plotting system similar to that of MATLAB.

import matplotlib.pyplot as plt

By running this special iPython command, we will be displaying plots inline:

%matplotlib inline

Plotting

The most important function in matplotlib is plot, which allows you to plot 2D data. Here is a simple example:

# Compute the x and y coordinates for points on a sine curve
x = np.arange(0, 3 * np.pi, 0.1)
y = np.sin(x)

# Plot the points using matplotlib
plt.plot(x, y)

[<matplotlib.lines.Line2D at 0x1142b94d0>]

png

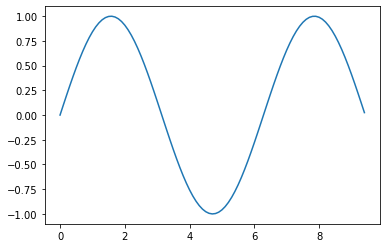
With just a little bit of extra work we can easily plot multiple lines at once, and add a title, legend, and axis labels:

y_sin = np.sin(x)
y_cos = np.cos(x)

# Plot the points using matplotlib
plt.plot(x, y_sin)
plt.plot(x, y_cos)
plt.xlabel('x axis label')
plt.ylabel('y axis label')
plt.title('Sine and Cosine')
plt.legend(['Sine', 'Cosine'])

<matplotlib.legend.Legend at 0x114390a50>

png

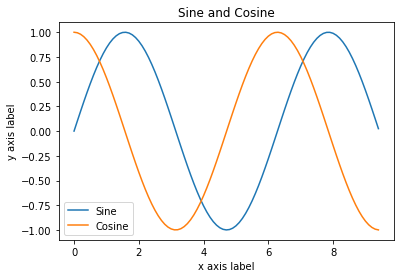
Subplots

You can plot different things in the same figure using the subplot function. Here is an example:

# Compute the x and y coordinates for points on sine and cosine curves
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)

# Set up a subplot grid that has height 2 and width 1,
# and set the first such subplot as active.
plt.subplot(2, 1, 1)

# Make the first plot
plt.plot(x, y_sin)
plt.title('Sine')

# Set the second subplot as active, and make the second plot.
plt.subplot(2, 1, 2)
plt.plot(x, y_cos)
plt.title('Cosine')

# Show the figure.
plt.show()

png

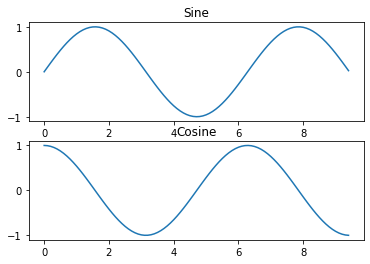
You can read much more about the subplot function in the documentation.

Holoviews

To be continued...

General requirements for Python code

Strict compliance with PEP8.
The length of the string is 79 characters.
The imports are properly sorted, there are no unused imports.
The margins are 4 spaces.
Hyphenation with correct indentation.
Backslashes are not used for transfers.
Consistency (the same quotes, the same methods of solving the same problems, and so on).
Lack of commented code and standard comments (# Create your views here. etc.).
Comments on functions are formatted as Docstrings, in accordance with the Docstring Conventions: Begin with a capital letter, end with a period, and contain a description of what the function does.
The comments to the code are concise and informative.
Long pieces of code are logically separated by blank lines like paragraphs in a text.
There are no unnecessary operations.
There are no extra else where they are not needed (if a return/raise occurs in the if); Guard Block is used
There are no unnecessary files in the repository: no pycache , .vscode and other things.
The executable code in .py files must be closed with the if name == ‘main’ construction.
For immutable sequences of data, tuples rather than lists are preferable.
In f-strings, only variable substitution is used and there are no logical or arithmetic operations, function calls, or similar dynamics.
Variables are named according to their meaning, in English, there are no single-letter names and transliteration. The variable name should not contain its type. If necessary, type annotations are used.

Полезные ссылки

Этот материал посвящён фундаментальным темам операционной системы Linux: процессу загрузки и организации файловых систем, инструментам консоли и внутреннему устройству. Понимание этих процессов необходимо для администрирования систем и решения возникающих проблем.

Загрузка

1. BIOS (Basic Input/Output System)

BIOS — это микропрограмма, хранящаяся на чипе материнской платы (во FLASH-памяти). При включении питания процессор выполняет первую инструкцию по адресу 0xFFFFFFF0 (так называемый reset vector), который указывает на код BIOS.

Основные функции BIOS:

POST (Power-On Self-Test): Проверка целостности самой микропрограммы, инициализация критически важного оборудования (процессор, память, чипсет), запуск встроенного ПО других устройств (видеокарта, сетевая карта).
Сигналы POST: Если на этапе самотестирования возникает ошибка, BIOS подаёт сигналы через системный динамик (например, 1 короткий — успех, длинные и короткие комбинации — различные ошибки).

2. Загрузчик (Bootloader)

Задача загрузчика — найти, загрузить в оперативную память и передать управление ядру операционной системы.

Схемы загрузки

BIOS + MBR (Master Boot Record):
- MBR — это первые 512 байт на диске. Содержит:
  - Bootstrap Code (446 байт) — первичный код загрузчика.
  - Partition Table (64 байта) — таблица разделов (до 4 первичных).
  - Signature (2 байта) — сигнатура 55 AA.
- Ограничение MBR: работа с дисками до 2 ТБ.
- Процесс: BIOS загружает MBR, код из MBR находит активный раздел и загружает следующий этап загрузчика (например, GRUB2), который уже находится в этом разделе.
UEFI + GPT (GUID Partition Table):
- UEFI — современный стандарт, пришедший на смену BIOS. Умеет читать файловые системы (например, FAT32) и поддерживает безопасную загрузку (Secure Boot).
- GPT — современная схема разделов, не имеющая ограничений MBR.
- Процесс: UEFI напрямую обращается к специальному FAT32-разделу (EFI System Partition), где хранятся файлы загрузчиков с расширением .efi (например, grubx64.efi). Загрузочные записи хранятся в NVRAM.

Полезные команды:

Просмотр UEFI-записей: efibootmgr -v
Просмотр разделов: fdisk -l

GRUB2 (Grand Unified Bootloader 2)

Самый распространённый загрузчик в Linux.

Позволяет выбирать ядро или ОС для загрузки.
Загружает необходимые модули для поддержки оборудования и файловых систем.
Основной конфигурационный файл: /boot/grub/grub.cfg (генерируется автоматически).

3. Ядро (Kernel)

Ядро Linux — это сжатый исполняемый файл (обычно vmlinuz-<версия> в каталоге /boot).

GRUB загружает ядро в оперативную память.
Ядро распаковывается.
Ядро запускается с параметрами командной строки (можно посмотреть в /proc/cmdline).
Ядро монтирует в памяти начальную RAM-диск (initramfs).

Initramfs (Initial RAM File System)

Это временная корневая файловая система в памяти.

Содержит необходимые на раннем этапе загрузки драйверы, модули ядра, микрокод и скрипты.
Его главная задача — смонтировать реальную корневую файловую систему (/), после чего управление передаётся процессу init.

4. Init и systemd

Процесс с PID 1 (init или systemd) является родителем для всех остальных процессов в системе.

Его основные задачи:

Управление порядком запуска служб (демонов).
Монтирование файловых систем (согласно /etc/fstab).
Управление всеми запущенными процессами.

systemd — современная и самая распространённая реализация init.

Использует концепцию юнитов (units) (сервисы, монтирования, сокеты и т.д.).
Позволяет просматривать зависимости: systemctl list-dependencies default.target
Имеет множество утилит для управления системой (systemctl, journalctl и др.).

Файловые системы

1. Немного о дисках

Жёсткий диск состоит из пластин, разделённых на дорожки и секторы (обычно по 512 байт или 4 КБ). Файловая система располагается внутри раздела диска, который описывается в таблице разделов (MBR или GPT).

2. Задачи файловой системы

ФС решает несколько ключевых задач:

Индексация и поиск данных (через структуры вроде inode).
Управление свободным пространством.
Контроль доступа (права, ACL).
Оптимизация производительности (кеширование, дефрагментация*).
Надёжность (журналирование).

*Дефрагментация менее критична для современных ФС (ext4, XFS, btrfs) и SSD.

3. Виды файловых систем

Доступ к разным ФС в Linux обеспечивается единым интерфейсом — VFS (Virtual File System).

FAT (File Allocation Table)

Плюсы: Простая, поддерживается всеми ОС.
Минусы: Нет журналирования, ограничения на размер файла и раздела (FAT32: файл до 4 ГБ, раздел до 32 ГБ).
Расчёт размера: FAT12: 2^12 * размер_блока.

ext4 (Fourth Extended Filesystem)

Стандарт для Ubuntu, Debian и многих других дистрибутивов.
Журналируемая — повышает надёжность, записывая метаданные операций в специальный журнал перед их выполнением.
Использует экстенты (extents) для более эффективного хранения больших файлов (вместо прямых/косвенных блоков).
Иноды (inodes) хранят метаданные о файле (права, владелец, указатели на данные). Их количество ограничено и задаётся при создании ФС.

XFS

Высокопроизводительная ФС, хорошо подходит для работы с большими файлами.
Использует B+-tree для индексации.
Отложенная аллокация — улучшает производительность.
Динамическое создание inodes.
Стандарт для Red Hat Enterprise Linux.

btrfs (B-Tree File System)

Современная ФС с продвинутыми функциями.
Copy-on-Write (CoW): При изменении файла данные записываются в новое место, а не перезаписываются старые. Это позволяет эффективно создавать снапшоты (snapshots).
Встроенная поддержка RAID и LVM-подобных функций.
Субаллокация — эффективная работа с маленькими файлами.
Поддержка TRIM для SSD.
Стандарт для openSUSE.

4. Конфигурирование файловой системы

Кеширование: Ядро использует Page Cache (для данных) и Dirty Cache (для изменённых, но не записанных данных) для ускорения работы.
I/O планировщики: Определяют порядок обработки запросов к диску. Доступны через /sys/block/<device>/queue/scheduler.
- cfq / bfq — «честное» распределение.
- deadline — учитывает сроки выполнения запросов.
- noop — простой FIFO (часто лучше для SSD).

Утилиты для работы с ФС:

mkfs, mke2fs — создание ФС.
tune2fs — изменение параметров ФС ext*.
debugfs — отладка ФС ext*.
fsck — проверка и восстановление ФС.

5. Монтирование

Процесс подключения раздела диска к определённой точке в дереве каталогов (/mnt, /home и т.д.).

Команды: mount, umount.
/etc/fstab — файл статической информации о файловых системах для автоматического монтирования при загрузке.
```
# Пример строки в /etc/fstab
UUID=ed465c6e-949a-41c6-8e8b-c8da348a3577 / ext4 defaults 0 1
```
Параметры монтирования: rw/ro (чтение/запись), noatime (не обновлять время доступа для производительности), acl (поддержка списков контроля доступа) и др.
systemd.mount — альтернатива fstab через юниты systemd.

6. RAID (Redundant Array of Independent Disks)

Технология объединения нескольких дисков в массив для повышения надёжности и/или производительности.

Уровень	Принцип	Надёжность	Производительность	Ёмкость
RAID 0	Striping (чередование)	Низкая	Высокая (чт/зап)	N
RAID 1	Mirroring (зеркалирование)	Высокая	Высокая (чт)	N/2
RAID 5	Четность	Средняя	Высокая (чт)	N-1
RAID 6	Двойная четность	Высокая	Высокая (чт)	N-2
RAID 10	Зеркалирование + чередование	Высокая	Высокая (чт/зап)	N/2

Создание программного RAID в Linux: Используется утилита mdadm.

# Пример создания RAID 1
mdadm --create /dev/md0 --level=1 --raid-devices=2 /dev/sdb /dev/sdc
mkfs.ext4 /dev/md0
mount /dev/md0 /mnt/raid
# Сохранение конфигурации
mdadm --detail --scan >> /etc/mdadm/mdadm.conf

7. LVM (Logical Volume Manager)

Система управления дисковым пространством, которая абстрагируется от физических дисков.

Преимущества LVM:

Гибкое управление размерами: Легко увеличивать, уменьшать логические тома.
Снапшоты: Возможность создания моментальных снимков томов.
Объединение дисков: Создание томов, размер которых превышает один физический диск.

Основные понятия:

Physical Volume (PV): Физический диск или раздел.
Volume Group (VG): Группа физических томов.
Logical Volume (LV): Логический том, создаваемый из пространства VG.

Основные команды:

pvcreate /dev/sdX — создать физический том.
vgcreate my_vg /dev/sdX1 /dev/sdY1 — создать группу томов.
lvcreate -n my_vol -L 10G my_vg — создать логический том размером 10 ГБ.
mkfs.ext4 /dev/my_vg/my_vol — создать ФС на томе.

Заключение

Понимание процесса загрузки и принципов работы файловых систем — ключевой навык для системного администратора Linux. Эти знания позволяют эффективно управлять системой, настраивать её под конкретные задачи, устранять неполадки и обеспечивать надёжность хранения данных.

Инструменты Linux

Лекция посвящена основным инструментам для эффективной работы в Linux-терминале. Мы рассмотрим всё: от настройки окружения до продвинутых методов диагностики проблем.

Часть 1: Подготовка и окружение

Слепая печать

Первый и самый важный навык — умение печатать, не глядя на клавиатуру.

Преимущества: Увеличение скорости, меньше ошибок, полный контроль над терминалом.
Сложности: Первые месяцы будут тяжелыми, но результат того стоит.

Инструменты для тренировки:

GNU Typist (gtypist) — консольный тренажер. Устанавливается через apt-get install gtypist или brew install gtypist.
monkeytype — современный онлайн-тренажер.
www.keybr.com — еще один популярный онлайн-тренажер.

Эмулятор терминала

Стандартные терминалы часто бедны на функции. Хороший терминал должен иметь:

Вкладки (табы).
Разделение окна (split panels).
Копирование в буфер обмена просто при выделении текста.
Поддержка кликабельных ссылок.
Система плагинов для расширения функционала.
Прочие "рюшечки" (темы, прозрачность и т.д.).

Рекомендуемые терминалы:

macOS: iTerm2
Linux: Terminator, Kitty, Konsole
Windows 10/11: Windows Terminal
Windows (условно-бесплатный): MobaXterm (также включает SSH-клиент, X-сервер и сетевые инструменты).

Моноширинные шрифты

Для удобства чтения кода в терминале необходимы качественные моноширинные шрифты.

Source Code Pro (Adobe)
Inconsolata (Google)
Anonymous Pro

Ссылки для скачивания приведены в презентации.

Командные оболочки (Shell)

Это интерпретатор команд, с которым вы взаимодействуете в терминале.

bash (Bourne-Again SHell): Универсальный стандарт. Лучший выбор для разнородной инфраструктуры.
zsh (Z Shell): Обладает расширенными возможностями и богатой экосистемой плагинов. Идеален для локальной разработки и контролируемой инфраструктуры. Фреймворк Oh My Zsh делает настройку zsh простой и приятной.
fish (Friendly Interactive SHell): Современный shell с удобством "из коробки". Выбирается по тем же причинам, что и zsh.

Часть 2: Основы командной строки

Структура команд

syscall exec — ищет исполняемый файл по путям, указанным в переменной окружения $PATH.
which <команда> или type <команда> — показывают полный путь к исполняемому файлу команды. Флаг -a покажет все возможные пути в $PATH.
Флаги команд не стандартизированы, но есть соглашения:
- -v / --version — показать версию.
- -h / --help — показать справку.
- -y / -f — пропустить подтверждение (yes/force).

Справка `man`

Основной источник информации — команда man (manual).

Пейджер: По умолчанию для просмотра используется less. Можно изменить переменной окружения $MANPAGER (например, MANPAGER=cat).
Основные клавиши в less:
- h — помощь.
- PgUp, PgDown, ↓, ↑ — навигация.
- /KEYWORD — поиск.
- N, n — переход к следующему/предыдущему совпадению.
- g — в начало документа.
- G — в конец документа.
man <раздел> <команда> — например, man 1 bash (справка по bash из раздела "пользовательские команды").
man -P 'less +/KEYWORD' bash — открыть man с поиском по ключевому слову.

Управление процессами

Ctrl + C — послать сигнал SIGINT (завершение процесса).
Ctrl + \ — послать сигнал SIGQUIT (завершение с дампом памяти).
Ctrl + Z — послать сигнал SIGTSTP (приостановка процесса).
fg — вернуть приостановленный процесс на передний план.
bg — запустить приостановленный процесс в фоновом режиме.
stty -a — посмотреть и перенастроить настройки терминала.

Управление вводом/выводом (I/O Redirection)

Потоки данных:
- stdin (0) — стандартный вход.
- stdout (1) — стандартный выход.
- stderr (2) — стандартный вывод ошибок.
Перенаправление:
- команда > файл — записать stdout в файл (перезаписать).
- команда >> файл — дописать stdout в конец файла.
- команда 2> файл — записать stderr в файл.
- команда &> файл — записать stdout и stderr в файл.
- команда 2>&1 — перенаправить stderr в stdout.
- команда | другая_команда — передать stdout первой команды на stdin второй.
Специальные файлы:
- /dev/null — "черная дыра".
- /dev/zero — источник нулей.
- /dev/urandom — источник псевдослучайных чисел.

Полезные помощники

Автодополнение (completion): Клавиша TAB — ваш лучший друг.
- Одно нажатие — дополнить команду/файл.
- Двойное нажатие — показать все возможные варианты.
История команд (~/.bash_history, ~/.zsh_history):
- Ctrl + R — реверсивный поиск по истории.
- history | grep <ключевое_слово> — поиск по истории.
- sudo !! — выполнить предыдущую команду с sudo.
- !$ — подставить последний аргумент предыдущей команды.

Ветвления, циклы и подоболочки (Subshell)

; — разделитель команд (выполняются последовательно).

Циклы и условия:

while true; do ...; done
for i in $(seq 1 10); do echo $i; done
if [ $(wc -l file.txt) -gt 3 ]; then ...; fi

read — встроенная команда для чтения ввода в переменные.
Подоболочка (Command Substitution):
- $(команда) или `команда` — вывод команды подставляется в строку.
[ — это бинарник, а не синтаксис shell. Подробнее: man [ или man test.

Часть 3: Полезные команды и утилиты

Find и многопоточность

find — мощный поиск файлов и директорий.
- Пример: find /etc -type f -name "nginx*"
xargs — передает результаты из stdin в аргументы другой команды.
- -P <N> — запуск до N процессов параллельно.
- -n1 — передавать по одному аргументу за раз.
- Пример: find ... | xargs -P10 -n1 md5sum
GNU parallel — более мощная альтернатива xargs для параллельного выполнения.

Управление сессиями: screen и tmux

Позволяют запускать процессы, которые продолжают работать после разрыва соединения.

screen:
- screen — создать новую сессию.
- Ctrl + A, D — отключиться от сессии (detach).
- screen -ls — список сессий.
- screen -r <session> — подключиться к сессии.
tmux (рекомендуется):
- tmux — создать сессию.
- Ctrl + B, D — отключиться.
- tmux ls — список сессий.
- tmux a -t <session> — подключиться.
- Интеграция с iTerm2: tmux -CC.
watch -d -n1 "команда" — выполняет команду раз в секунду и подсвечивает различия.

Редактирование текста

Vim:
- Мощный, вездесущий, имеет крутую кривую обучения.
- vimtutor — встроенный интерактивный учебник. Пройдите его!
- Основы: i — вход в режим вставки, ESC — возврат в нормальный режим, :wq — сохранить и выйти, :q! — выйти без сохранения.
- vimdiff file1 file2 — сравнение файлов.
Emacs: Другой мощный редактор. "Если вы знаете, что это, скорее всего, вам не нужна эта лекция".
Система контроля версий Git: Обязательный инструмент для любой современной IT-профессии.

Потоковая обработка текста

Мощные утилиты для фильтрации и преобразования текстовых потоков. Не используйте их для построения продакшен-процессов!

grep — фильтрация строк по регулярному выражению.
awk — целый язык для обработки текста, основанный на колонках.
sed — потоковый текстовый редактор (замена, удаление строк и т.д.).
cut — извлечение конкретных колонок.
head / tail — вывод начала/конца файла.
tr — замена или удаление символов.
wc — подсчет строк, слов, символов.
sort — сортировка строк.
uniq — фильтрация повторяющихся строк.

Тренажеры: grepexercises, sedexercises, awkexercises (устанавливаются через pip).

Практика: The Command Line Murders — текстовый квест в терминале для отработки навыков. (https://github.com/veltman/clmystery)

Часть 4: Диагностика и поиск проблем

Методология и ресурсы

Брендан Грегг (Brendan Gregg) — гуру производительности.
Его сайт — кладезь информации: https://www.brendangregg.com/linuxperf.html
Книга "Systems Performance: Enterprise and the Cloud" — must-read для углубленного изучения.

На его сайте можно найти бесценные диаграммы выбора инструментов:

Linux Observability Tools
Linux Static Performance Tools
Linux Benchmarking Tools
Linux Tuning Tools

Мини-топ полезных утилит

Мониторинг процессов и системы:
- top / htop — интерактивный просмотр процессов.
- atop — расширенный мониторинг, может записывать данные в файл.
- pidof — найти PID по имени процесса.
- ps fauxw | less — детальный список процессов.
Диски и файловая система:
- df -h / df -ih — место на дисках и inodes.
- du -sh /path/* — размер директорий.
- iostat -x 1 — статистика ввода-вывода.
Сеть:
- ss -s / netstat -ntlp — статистика сокетов и открытые порты.
- ping / traceroute / mtr — диагностика сетевой связности.
- tcpdump — "сниффер" сетевых пакетов.
- ethtool eth0 — настройки и статистика сетевого интерфейса.
Прочее:
- lsof -i:포트 / lsof -p $PID — список открытых файлов сокетов процессом.
- strace -fp $PID / strace $cmd — трассировка системных вызовов.
- dmesg -T — просмотр логов ядра.
- perf top -F99 — профилирование системы в реальном времени.
- curl — мастер на все руки для работы с HTTP/сетью.

Заключение

Освоение терминала и его инструментов — это путь к настоящей эффективности в Linux. Начинайте с основ: печать, терминал, справка man. Постепенно внедряйте в свою практику более сложные инструменты, такие как vim, tmux, grep, awk и sed. Не бойтесь экспериментировать и использовать ресурсы, подобные сайту Брендана Грегга, для углубления знаний.

Удачи в освоении мощного мира Linux-инструментов!

Коды и скрипты

Здесь рассмотрим примеры программного обеспечения, созданные мной и моими коллегами.

Уравнение огибающей Капчинского-Владимирского для пучка заряженных частиц

Сначала разберем теорию, а затем расчитаем огибающую электронного пучка в линейном ускорителе с помощью Python.

Уравнения Максвелла

Объемная плотность тока пучка $\jmath = \rho\upsilon$, где $\rho$ - объемная плотность заряда, $\upsilon$ - скорость пучка. Запишем дифференциальные уравнения Максвелла: $$ \nabla \vec{D} = 4\pi\rho, $$ $$ \nabla\times \vec{H} = \frac{4\pi\vec{\jmath}}{c}, $$ где $\vec{D}$ - индукция электрического поля, $\vec{H}$ - напряженность магнитного поля, $с$ - скорость света. Используем теорему Стокса об интегрировании дифференциальных форм, чтобы получить уравнения Максвелла в интегральной форме: $$ \oint\limits_{\eth V} \vec{D}\vec{dS} = 4\pi\int\limits_V\rho{dV}, $$ $$ \oint\limits_{\eth S} \vec{H}\vec{dl} = \frac{4\pi}{c}\int\limits_S\vec{\jmath}\vec{dS}. $$

Найдем $D_r$ для цилиндрического пучка радиуса $a$ с постоянной плотностью $\rho_0$: $$ D_r = \frac{4\pi}{r}\int\limits^r_0\rho(\xi)\xi d\xi = \begin{equation*} \begin{cases} \displaystyle 2\pi\rho_0 r, r < a, \ \displaystyle \frac{2\pi\rho_0 a^2}{r}, r > a. \end{cases} \end{equation*} $$

Учитывая, что в вакууме $D = E$, $H = B$, $E$ - напряженность электрического поля, $B$ - индукция магнитного поля, и в плоском пространстве в декартовой системе координат $H_\alpha = \beta D_r$, где $\displaystyle\beta = \frac{\upsilon}{c}$, радиальная компонента силы $F_r$ из силы Лоренца $\vec{F} = e\vec{E} + \displaystyle\frac{e}{c}\vec{\upsilon}\times\vec{B}$ : $$ F_r = eE_r - \frac{e\upsilon_z B_\alpha}{c} = eE_r(1-\displaystyle \frac{\upsilon^2}{c^2}) = \displaystyle \frac{eE_r}{\gamma^2}. $$ Полезно выразить поле через ток $$ I = \rho_0\upsilon\pi a^2, $$ тогда: $$ E_r = \begin{equation*} \begin{cases} \displaystyle \frac{2 I r}{a^2\upsilon}, r < a, \ \displaystyle \frac{2 I}{r\upsilon}, r > a. \end{cases} \end{equation*} $$

Уравнения движения

Второй закон Ньютона $\dot p_r = F_r$, используем параксиальное приближение и считаем $\gamma = const$: $$ \gamma m \ddot r = \displaystyle \frac{eE_r}{\gamma^2} = \displaystyle \frac{2 I e}{\gamma^2 a^2 \upsilon} r, $$ получилось линейное уравнение, но так как все частицы движутся нужно учесть, что $a = a(t)$. Решение линейного уравнения можно представить как линейное преобразование фазовой плоскости. Так как отрезок на фазовой плоскости при невырожденном линейном преобразовании переходит в отрезок, то его можно охарактеризовать одной точкой. Следовательно, выберем крайнюю точку $r = a$, которая будет характеризовать крайнюю траекторию: $$ \gamma m \ddot r = \displaystyle \frac{2 I e}{\gamma^2 a \upsilon}. $$ Перейдем к дифференцированию по $z$, учтем, что $\displaystyle dt = \frac{dz}{v}$, тогда: $$ a'' = \displaystyle \frac{e}{a}\frac{2I}{m\gamma^3\upsilon^3}. $$ Введем характерный альфвеновский ток $I_a = \displaystyle \frac{mc^3}{e} \approx$ 17 kA, следовательно: $$ a'' = \displaystyle \frac{2I}{I_a (\beta\gamma)^3} \frac{1}{a}. $$ Учтем внешнюю фокусировку, предполагая суперпозицию полей (верно не всегда, например, в нелинейных средах это не выполняется), получим: $$ a'' + k(z)a - \displaystyle \frac{2I}{I_a (\beta\gamma)^3} \frac{1}{a} = 0, $$ что напоминает уравнение огибающей: $$ w'' + kw - \displaystyle \frac{1}{w^3} = 0 ,$$ где $ w =\displaystyle \sqrt \beta .$

Уравнения огибающей для эллиптического пучка с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями

Распределение Капчинского-Владимирского: $$ f = A\delta(1 - \displaystyle\frac{\beta_x x'^2 + 2\alpha_x x x' + \gamma_x x^2}{\epsilon_x} - \displaystyle\frac{\beta_y y'^2 + 2\alpha_y y y' + \gamma_y y^2}{\epsilon_y} ), $$ где $А$ - инвариант Куранта-Снайдера. Полуоси эллипса: $$ a = \sqrt{\epsilon_x \beta_x}, b = \sqrt{\epsilon_y \beta_y}. $$ Поле получается линейно внутри заряженного эллиптического цилиндра: $$ E_x = \displaystyle \frac{4I}{\upsilon}\frac{x}{a(a+b)}, $$ $$ E_y = \displaystyle \frac{4I}{\upsilon}\frac{y}{b(a+b)}. $$ Проверим, что $\nabla \vec{E} = 4\pi\rho:$ $$ \displaystyle I = \rho \upsilon \pi ab, $$ $$ \nabla \vec{E} = \displaystyle \frac{4I(a+b)}{\pi(a+b)ab} = \displaystyle \frac{4I}{\pi ab} = 4\pi\rho. $$ Так как поля линейные, они добавятся к полям фокусирующей линзы. Подставим в уравнение огибающей $\displaystyle a = \sqrt \epsilon_x w_x, b = \sqrt \epsilon_y w_y:$ $$ a'' + k_{xt} a - \frac{\epsilon_x^2}{a^3} = 0, $$ где $k_{xt} = k_x + k_{xsc}$ - полная жесткость, $k_x$ - жесткость линзы, а $\displaystyle k_{xsc} = \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{a(a+b)}.$ В итоге получаем систему уравнений, связанных через пространственный заряд: $$ \begin{equation*} \begin{cases} \displaystyle a'' + k_xa - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_x^2}{a^3} = 0 , \\ \displaystyle b'' + k_yb - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_y^2}{b^3} = 0. \end{cases} \end{equation*} $$

Количественный критерий применимости приближения ламинарности течения

Данная система уравнений позволяет учесть 2 эффекта, мешающих сфокусировать пучок в точку - конечность эммитанса и пространственный заряд. Работают члены одинаково, поэтому можно сравнить эти величины. Когда ток $I$ малый - слабое отталкивание, если ток $I$ большой - сильное отталкивание, следовательно, эммитанс можно откинуть и считать течение ламинарным. Очевидно, количественный критерий применимости ламинарности течения выглядит так: $$ \displaystyle \sqrt{\frac{2I}{I_a(\beta\gamma)^3}} \gg \sqrt{\frac{\epsilon}{\beta}}. $$ Видно, что пространственный заряд влияет на огибающую больше там, где $\beta$-функция больше, а в вблизи фокуса влиянием пространственного заряда можно пренебречь.

Теорема Буша

В качестве дополнения к выводу уравнения огибающей пучка докажем важную вспомогательную теорему, которая называется теоремой Буша. Она связывает угловую скорость заряженной частицы, движущейся в аксиально-симметричном магнитном поле, с магнитным потоком, охваченным окружностью с центром на оси и проходящим через точку, в которой расположена частица.

Рассмотрим заряд $q$, движущийся в магнитном поле $\vec B = (B_r,0,B_z)$. Приравняем $\theta$ - составляющую силы Лоренца к производной момента импульса по времени, деленной на $r$: $$ F_\theta = -q(\ddot r B_z - \dot z B_r) = \frac{d}{rdt}(\gamma m r^2 \dot \theta). $$ Поток, пронизывающий площадь, охваченную окружностью радиуса $r$, центр которой расположен на оси, а сама она проходит через точку, в которой расположен заряд, записывается в виде $\psi = \int\limits^r_0 2\pi r B_z dr$. Когда частица перемещается на $\vec{dl} = (dr,dz)$, скорость изменения потока, охваченного этой окружностью, можно найти из второго уравнения Максвелла $\nabla \vec{B} = 0.$ Таким образом, $$ \dot\psi = 2\pi r (-B_r \dot z + B_z \dot r). $$ После интегрирования по времени из приведенных уравнений получаем следующее выражение: $$ \dot \theta = (-\frac{q}{2\pi \gamma m r^2})(\psi - \psi_0). $$

Уравнение параксиального луча

Здесь мы запишем уравнение параксиального луча в виде, соответсвующем системе с аксиальнорй симметрией при принятых ранее допущениях. Чтобы вывести уравнение параксиального луча, приравняем силу радиального ускорения силам электрическим и магнитным со стороны внешних полей. Нужно помнить, что величина $\gamma = \gamma(t).$ $$ \frac{d}{dt}(\gamma m \dot r) - \gamma m r (\dot \theta)^2 = q(E_r + r\dot \theta B_z). $$ Применим теорему Буша и независимость $B_z$ от $r:$ $$ -\dot \theta = \frac{q}{2\gamma m}(B_z - \frac{\psi_0}{\pi r}). $$ Исключим $\dot \theta$ и подставим $\displaystyle \dot \gamma \approx \frac {\beta q E_z }{mc}:$ $$ \ddot r + \frac{\beta q E_z}{\gamma m c} \dot r + \frac{q^2 B^2_z}{4\gamma ^2 m^2} r - \frac{ q^2 \psi^2_0}{4\pi^2\gamma^2 m^2} (\frac{1}{r^3}) - \frac{q E_r}{\gamma m } = 0. $$

Уравнение огибающей для круглого и эллиптического пучка

Учитывая, что: $$ \dot r = \beta c r', $$ $$ \ddot r = r'' (\dot z)^2 + r'\ddot z \approx r'' \beta^2 c^2 + r' \beta' \beta c^2. $$ А также, если в области пучка нет никаких зарядов, то, разлагая в ряд Тейлора в окрестности оси и оставляя только первый член, с учетом $$\nabla \vec{E} = 0$$ получаем $$ E_r = -0.5 r E'_z \approx - 0.5 r \gamma'' mc^2/q. $$ Тогда окончательно можем записать уравнение огибающей для круглого пучка радиуса $r$ с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями: $$ \displaystyle r'' + \frac{1}{\beta^2\gamma} \gamma' r' + \frac{1}{2\beta^2\gamma}\gamma''r + kr - \frac{2I}{I_a (\beta\gamma)^3}\frac{1}{r} - \frac{\epsilon^2}{r^3} = 0 ; $$ и для эллиптического пучка: $$ \begin{equation*} \begin{cases} \displaystyle a'' + \frac{1}{\beta^2\gamma} \gamma' a' + \frac{1}{2\beta^2\gamma}\gamma''a + k_xa - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_x^2}{a^3} = 0 , \\ \displaystyle b'' + \frac{1}{\beta^2\gamma} \gamma' b' + \frac{1}{2\beta^2\gamma}\gamma''b + k_yb - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_y^2}{b^3} = 0. \end{cases} \end{equation*} $$

Магнитные линзы

Фокусирующими элементами могут являться: соленоиды и магнитные квадрупольные линзы.

Соленоиды

$k_x = k_y = k_s$ - жесткость соленоида: $$ k_s = \left ( \frac{eB_z}{2m_ec\beta\gamma} \right )^2 = \left ( \frac{e B_z}{2\beta\gamma\cdot 0.511\cdot 10^6 e \cdot \mathrm{volt}/c} \right )^2 = \left ( \frac{cB_z[\mathrm{T}]}{2\beta\gamma\cdot 0.511\cdot 10^6 \cdot \mathrm{volt}} \right )^2. $$

Квадруполи

$k_q = \displaystyle\frac{eG}{pc}$ - жесткость квадруполя, где $G = \displaystyle\frac{\partial B_x}{\partial y} = \displaystyle\frac{\partial B_y}{\partial x}$ - градиент магнитного поля, причем $k_x = k_q, k_y = -k_q.$ $$ k_q = \left ( \frac{eG}{m_ec\beta\gamma} \right ) = \left ( \frac{eG}{\beta\gamma\cdot 0.511\cdot 10^6 e \cdot \mathrm{volt}/c} \right ) = \left ( \frac{cG}{\beta\gamma\cdot 0.511\cdot 10^6 \cdot \mathrm{volt}} \right ). $$

Продольная динамика пучка

Уравнение на продольную динамику пучка можно решить независимо от уравнения на огибающую, чтобы в уравнении на огибающую уже использовать готовую функцию энергии пучка от $z$. Считая, что скорость электрона достаточно близка к скорости света и следовательно его продольная координата $z \approx ct$, а импульс $p_z \approx \gamma mc$

$$ \frac{d\gamma}{dz} \approx \frac{eE_z}{mc^2}, $$

Тогда достаточно один раз проинтегрировать функцию $E_z(z)$:

Решение уравнения огибающей для эллиптического пучка с фокусирующими элементами

Уравнение огибающей для эллиптического пучка с полуосями $a, b$ с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями: $$ \begin{equation*} \begin{cases} \displaystyle a'' + \frac{1}{\beta^2\gamma} \gamma' a' + \frac{1}{2\beta^2\gamma}\gamma''a + k_qa - \frac{2P}{(a+b)} - \frac{\epsilon_x^2}{a^3} = 0 , \\ \displaystyle b'' + \frac{1}{\beta^2\gamma} \gamma' b' + \frac{1}{2\beta^2\gamma}\gamma''b - k_qb - \frac{2P}{(a+b)} - \frac{\epsilon_y^2}{b^3} = 0. \end{cases} \end{equation*} $$

Пусть $\displaystyle x = \frac{da}{dz}, y = \frac{db}{dz}, \displaystyle \frac{d\gamma }{dz}\approx \frac{e E_z}{m c^2}, k = \frac{1}{R} - $ кривизна, тогда $$ \begin{matrix} \displaystyle \frac{dx}{dz}= - \frac{1}{\beta^2\gamma} \gamma' a' - \frac{1}{2\beta^2\gamma}\gamma''a - k_qa + \frac{2P}{(a+b)} + \frac{\epsilon_x^2}{a^3}\\ \displaystyle\frac{da}{dz} = x\\ \displaystyle \frac{dy}{dz}= - \frac{1}{\beta^2\gamma} \gamma' b' - \frac{1}{2\beta^2\gamma}\gamma''b + k_qb + \frac{2P}{(a+b)} + \frac{\epsilon_x^2}{b^3}\\ \displaystyle\frac{db}{dz} = y \end{matrix}. $$ Пусть $\vec X = \begin{bmatrix} x \\ a \\ y \\ b \end{bmatrix} $, теперь составим дифференциальное уравнение $X' = F(X).$

Уравнение траектории для одной частицы

Векторный потенциал в соленоиде имеет только одну компоненту и легко выражается через $B_z(z)$: $$ A_\phi (z,r)=\sum_0^{inf} \dfrac{(-1)^n}{n!(n+1)!} B_z^{2n}(\dfrac{r}{2})^{2n+1/2}. $$ Следовательно Лагранжиан в цилиндрической системе координат имеет вид: $$ L = -mc^2(1-\beta^2)^{1/2} + \dfrac{e}{c}A_\phi r \dot\phi. $$ Из аксиальной симметрии следует существование интеграла движения: $$ P_\phi = \gamma mr^2\dot\phi + \dfrac{e}{c} r A_\phi = \gamma mr^2\dot\phi_0. $$ Продифференцировав по $z$ получим: $$ \phi' - \phi_0' = -\dfrac{e}{pc}\dfrac{A_\phi}{r}. $$ И в параксиальном приближении: $$ \phi' - \phi_0' = -\dfrac{e}{pc}B_z(z). $$ Откуда: $$ \delta \phi = \int\dfrac{e}{2pc}B_z(z)dz. $$ Тогда и уравнения траектории в приведенных координатах выглядят так: $$ \begin{equation*} \begin{cases} \displaystyle \tilde x'' + \frac{1}{\beta^2\gamma} \gamma'\tilde x' + \frac{1}{2\beta^2\gamma}\gamma''\tilde x + k_s \tilde x = 0 , \\ \displaystyle \tilde y'' + \frac{1}{\beta^2\gamma} \gamma'\tilde y' + \frac{1}{2\beta^2\gamma}\gamma''\tilde y +k_s \tilde y = 0, \end{cases} \end{equation*} $$

Расчет в Python

Сначала подключим необходимые библиотеки и настроим параметры графики

import numpy as np
import holoviews as hv
hv.extension('matplotlib')

%output size=200 backend='matplotlib' fig='svg'

%opts Curve Scatter Area [fontsize={'title':14, 'xlabel':14, 'ylabel':14, 'ticks':14, 'legend': 14}]

%opts Area Curve [aspect=3 show_grid=True]
%opts Area  (linewidth=1 alpha=0.25)
%opts Curve (linewidth=2 alpha=0.5)

import warnings
warnings.filterwarnings('ignore')

Настроим область и шаг счета

dz = 0.005 # m
z_min = 0.7
z_max = 15
z = np.arange(z_min,z_max,dz) # m

Определим элемент ускорителя (напр. соленоид, или ускоряющий зазор). Ускоритель будем представлять в виде последовательности таких элементов.

class Element:
  def __init__(self, z0, MaxField, filename, name):
    self.z0 = z0
    self.MaxField = MaxField
    self.filename = filename
    self.name = name

Фокусирующие соленоиды:

Bz_beamline = {}
for   z0,         B0,        filename,       name in [
    # m           T                          Unique name
    [ 0.95,       0.001,    'input/fields/B_z(z).dat', 'Sol. 1' ],
    [ 2.1,        0.03,     'input/fields/B_z(z).dat', 'Sol. 2' ],
    [ 2.9077,     0.001,    'input/fields/B_z(z).dat', 'Sol. 3' ],
    [ 4.0024,     0.03,     'input/fields/B_z(z).dat', 'Sol. 4' ],
    [ 5.642,      0.03,     'input/fields/B_z(z).dat', 'Sol. 5' ],
    [ 6.760,      0.001,    'input/fields/B_z(z).dat', 'Sol. 6' ],
]:
    Bz_beamline[name] = Element(z0, B0, filename, name)

Bz_beamline['Sol. 3'].z0

2.9077

Ускоряющие элементы:

Ez_beamline = {}
for   z0,          E0,       filename,      name in [
    # m            MV/m                     Unique name
    [ 7.456,       -0.9,     'input/fields/E_z(z).dat',  'Cavity 3'],
    [ 8.838,       -0.9,     'input/fields/E_z(z).dat',  'Cavity 4'],
    [ 10.220,      -0.9,     'input/fields/E_z(z).dat',  'Cavity 5'],
    [ 11.602,      -0.9,     'input/fields/E_z(z).dat',  'Cavity 6'],
    [ 12.984,      -0.9,     'input/fields/E_z(z).dat',  'Cavity 7'],
    [ 14.366,      -0.9,     'input/fields/E_z(z).dat',  'Cavity 8'], 
]:
    Ez_beamline[name] = Element(z0, E0, filename, name)

Считывание профилей фокусирующего и ускоряющего поля

Сперва мы просто считываем поля из файлов и сшиваем их в один массив:

from scipy import interpolate

FieldFiles = {} # buffer for field files
def read_field(beamline, z):
    global FieldFiles
    F = 0
    for element in beamline.values():
        if not (element.filename in FieldFiles):
            print('Reading ' + element.filename)
            FieldFiles[element.filename] = np.loadtxt(element.filename)
        M = FieldFiles[element.filename]
        z_data = M[:,0]
        F_data = M[:,1]
        f = interpolate.interp1d(
            element.z0+z_data, element.MaxField*F_data,
            fill_value=(0, 0), bounds_error=False
        )
        F = F + f(z)
    return F

Bz = read_field(Bz_beamline, z)

Reading input/fields/B_z(z).dat

Для интегрирования уравнения на огибающую необходимо сконвертировать массив Bz в функцию Bz(z)

Bz = interpolate.interp1d(z, Bz, fill_value=(0, 0), bounds_error=False)

Теперь Bz уже функция, которая быстро может вывести поле в любых точках вдоль ускорителя.

Bz(2.11111)

array(0.02984419)

Построим поле $Bz(z)$

dim_z  = hv.Dimension('z',  unit='m', range=(0,z_max))
dim_Bz = hv.Dimension('Bz', unit='T', label='$B_z$')

z_Bz = hv.Area((z,Bz(z)), kdims=dim_z, vdims=dim_Bz)
z_Bz

Аналогично для ускоряющего электрического поля:

Ez = 1*read_field(Ez_beamline, z)

Ez = interpolate.interp1d(z, Ez, fill_value=(0, 0), bounds_error=False)

dim_Ez = hv.Dimension('Ez', unit='MV/m', label=r'$E_z$')

z_Ez = hv.Area((z,Ez(z)), kdims=dim_z, vdims=dim_Ez)

z_Ez

Продольная динамика пучка

$$ \frac{d\gamma}{dz} \approx \frac{eE_z}{mc^2}, $$

Тогда достаточно один раз проинтегрировать функцию $E_z(z)$:

mc = 0.511 # MeV/c
#p_z = 2.459 # MeV/c
E_0 = 2.000 # MeV
gamma_0 = E_0/mc + 1 # Начальный релятивистский фактор пучка
#gamma_0 = p_z/mc

from scipy import integrate

gamma = gamma_0 + integrate.cumtrapz(-Ez(z)/mc, z)

dim_gamma = hv.Dimension('gamma', label=r'$\gamma$', range=(0,None))

z_gamma = hv.Curve((z,gamma), kdims=dim_z, vdims=dim_gamma)

(z_gamma + z_Ez).cols(1)

Для дальнейшего использования в решении уравнения на огибающую преобразуем массив gamma в функцию:

gamma = interpolate.interp1d(z[1:], gamma, fill_value=(gamma[0], gamma[-1]), bounds_error=False)

#hv.Curve((z,gamma(z)), kdims=dim_z, vdims=dim_gamma)

Решение уравнения огибающей для круглого пучка

Уравнение огибающей для круглого пучка радиуса $r$ с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями: $$ \displaystyle r'' + \frac{1}{\beta^2\gamma} \gamma' r' + \frac{1}{2\beta^2\gamma}\gamma''r + kr - \frac{2I}{I_a (\beta\gamma)^3}\frac{1}{r} - \frac{\epsilon^2}{r^3} = 0. $$

Перейдем к среднеквадратичному радиусу для распределения Капчинского-Владимирского и перевеансу $\displaystyle r_{rms} = \frac{r}{2}$ и $\displaystyle P = \frac{2I}{I_a\beta^3\gamma^3} $. Получим $$ \displaystyle r_{rms}'' + \frac{1}{\beta^2\gamma} \gamma' r_{rms}' + \frac{1}{2\beta^2\gamma}\gamma''r_{rms} + kr_{rms} - \frac{P}{4r_{rms}} - \frac{\epsilon^2}{16{r_{rms}}^3} = 0. $$

Пусть $\displaystyle y=\frac{dr_{rms}}{dz}, \displaystyle \frac{d\gamma }{dz}\approx \frac{e E_z}{m c^2}$, тогда $$ \begin{matrix} \displaystyle \frac{dy}{dz}= - \frac{1}{\beta^2\gamma} \gamma' r_{rms}' - \frac{1}{2\beta^2\gamma}\gamma''r_{rms} - kr_{rms} + \frac{P}{4r_{rms}} + \frac{\epsilon^2}{16r_{rms}^3}\\ \displaystyle\frac{dr_{rms}}{dz} = y \end{matrix}. $$ Пусть $\vec X = \begin{bmatrix} y \ r_{rms} \ \end{bmatrix} $, теперь составим дифференциальное уравнение $X' = F(X).$

$k$ - жесткость соленоида:$$ k = \left ( \frac{eB_z}{2m_ec\beta\gamma} \right )^2 = \left ( \frac{e B_z}{2\beta\gamma\cdot 0.511\cdot 10^6 e \cdot \mathrm{volt}/c} \right )^2 = \left ( \frac{cB_z[\mathrm{T}]}{2\beta\gamma\cdot 0.511\cdot 10^6 \cdot \mathrm{volt}} \right )^2. $$

c = 299792458 # (m/s) скорость света

Зададим начальные условия

I = 2000#2000.000 # A Ток в ускорителе    
Ia = 17000 # A Альфвеновский ток
emitt_n = 1.80e-4#1.80e-5 # m нормализованный эммитанс
R_rms = 27.5e-3 #m r_rms пучка
dR_rmsdz = 35.4e-3 #50e-3 dr_rms/dz пучка ## 50/2*sqrt(2) = 35.4

from scipy.integrate import odeint
from scipy.misc import derivative

def dXdz(X, z):
    
    y     = X[0]
    sigma = X[1]
    
    g = gamma(z)
    
    dgdz = Ez(z)/mc
    d2gdz2 = derivative(lambda z:Ez(z),z, dz)/mc
    beta = np.sqrt(1-1/(g*g))
    K = ( c * Bz(z) / (2*0.511e6))**2
    emitt = emitt_n/(g*beta) # m
    P=2*I/(Ia*beta*beta*beta*g*g*g)
    dydz = P/(4*sigma) + emitt*emitt/(sigma*sigma*sigma*16) - K*sigma/(g*beta)**2 - \
           dgdz*y/(beta*beta*g) - d2gdz2*sigma/(2*beta*beta*g)
    dsigmadz = y
    
    return [dydz, dsigmadz]

Функция решения уравнения на огибающую пучка:

def find_sigma(z):
    X0 = [dR_rmsdz, R_rms]      
    
    sol = odeint(dXdz, X0, z, rtol = 0.001) # rtol - относительная точность (по умолчанию rtol = 1.49012e-8)
    sigma = sol[:, 1] # m

    return sigma # m

%opts Area.Beam [aspect=3 show_grid=True] (color='red' linewidth=1 alpha=0.3)

sigma = find_sigma(z)

dim_sig = hv.Dimension('r_{rms}', label="$r_{rms}$", unit='mm', range=(0,150))

sigma_img = hv.Area((z,sigma*1e3), kdims=[dim_z], vdims=[dim_sig], group='Beam')
sigma_img